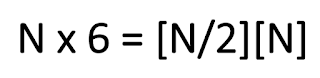To multiply any number with 6, put that number in ones position, and number/2 in tens (or greater than tens) position.
Basically,And this rule applies to both odd and even numbers.
Let's start with simple examples with even number first:
Example 1: 8 x 6Here, N = 8, and N/2 = 4
8 x 6 = [N/2][N] = 48
For even numbers N >= 10:
Example 2: 10 x 6
Here,
N = 10 ( 1 is a forward carry)
N/2 = 5 (+ carry)
10 x 6 = [N/2][N] = [5][10] = [5+1][0] = 60
Here,
N = 10 ( 1 is a forward carry)
N/2 = 5 (+ carry)
10 x 6 = [N/2][N] = [5][10] = [5+1][0] = 60
Example 3: 28 x 6
Here,
N = 28 ( 2 is a forward carry)
N/2 = 14 (+ carry)
28 x 6 = [N/2][N] = [14][28] = [14+2][8] = 168
Here,
N = 28 ( 2 is a forward carry)
N/2 = 14 (+ carry)
28 x 6 = [N/2][N] = [14][28] = [14+2][8] = 168
Example 4: 102 x 6
N = 102 ( 10 is a forward carry)
N/2 = 51 (+ carry)
102 x 6 = [N/2][N] = [51][102] = [51 + 10][2] = 612
N/2 = 51 (+ carry)
102 x 6 = [N/2][N] = [51][102] = [51 + 10][2] = 612
Example 5: 1234 x 6
N = 1234 ( 123 is a forward carry)
N/2 = 1234/2 = 617 (+ carry)
1234 x 6 = [N/2][N] = [617][1234] = [617 + 123][4] = 7404
N/2 = 1234/2 = 617 (+ carry)
1234 x 6 = [N/2][N] = [617][1234] = [617 + 123][4] = 7404
For odd numbers:
Multiplication of 6 with odd number can be seen as a special case.
One simple way to do is to do multiple with N-1, which will be an even number and then add 6.
N x 6 = (N-1) x 6 + 6
Another approach is to do it exactly the way it is done for even numbers. While the method remains the same, division by 2 brings a new dimension.
Example 6: 3 x 6
N = 3
N/2 = 3/2 = 1.5 ( where 5 is a backward carry )
3 x 6 = [N/2][N] = [1.5][3] = [1][5+3] = 18
N/2 = 3/2 = 1.5 ( where 5 is a backward carry )
3 x 6 = [N/2][N] = [1.5][3] = [1][5+3] = 18
Example 7: 47 x 6
N = 47 ( where 4 is a forward carry )
N/2 = 47/2 = 23.5 ( where 5 is a backward carry )
47 x 6 = [N/2][N] = [23.5][47] = [23 + 4][5+7] = [27][12] = [27 + 1][2] = 282
Note:
Example 8: 13579 x 6
N/2 = 47/2 = 23.5 ( where 5 is a backward carry )
47 x 6 = [N/2][N] = [23.5][47] = [23 + 4][5+7] = [27][12] = [27 + 1][2] = 282
Note:
- The highlighted step is an important one. When after adding backward carry, if the number in ones position is > 9, push front digits as a forward carry.
Example 8: 13579 x 6
N = 13579 ( where 1357 is a forward carry )
N/2 = 13579/2 = 6789.5 ( where 5 is a backward carry )
13579 x 6 = [N/2][N] = [6789.5][13579] = [6789 + 1357][5+9] = [8146][14] = [8146 + 1][4] = 81474
Example 10: 79 x 42
N/2 = 13579/2 = 6789.5 ( where 5 is a backward carry )
13579 x 6 = [N/2][N] = [6789.5][13579] = [6789 + 1357][5+9] = [8146][14] = [8146 + 1][4] = 81474
What's next?
Now, here we saw how the multiplication by number 6 can be simplified. And the method applies to both odd and even numbers.
But is there something more to it? Can it be extended to other numbers?
Well, the answer is, it can be extended to other numbers who are multiples of 6.
General rule is,
Where M=6 -> 12, M=2 -> 12, M=3 -> 24 ...
Let's take few examples to see how it works.
Example 9: 15 x 12
Here, N = 15, M = 2
Here, N = 15, M = 2
15 x 12 = [(NxM)/2][NxM] = [(15 x 2)/2][15 x 2] = [15][30] = [15 + 3][0] = 180
Here, N = 79, M = 7
79 x 42 = [(NxM)/2][NxM] = [(79 x 7)/2][79 x 7] = [276.5][553] = [276][5 + 553]
= [276][558] = [276 + 55][8] = 3318
= [276][558] = [276 + 55][8] = 3318